Then I gave what Ellie calls an "impromptu" speech about what the Differential Calculus is and what the Integral Calculus is, by giving a general overview of the limit of (one form of) the difference quotient, and then your first (right-endpoint version of) a Riemann Sum (The sigma thingie with the funny-looking "E," which is actually the Greek letter "S," which stands for "sum.), of which we took the limit as the width of the rectangles approached zero.

After that, I left people to their own devices. Only 2 people stayed. I was hoping more would use that time to get work done, but all but 2 made a quick getaway. Then we 3 hung out. There were some spans of several minutes when nobody said anything, and then there was a flurry of questions! Cool!

I ended up working 3 or 4 more or less standard difference quotients of medium-to-high difficulty, including

• Quadratic Function
• Square Root Function
• Cubed Function - Required knowledge of Binomial cubed. Introduced Pascal's Triangle version of the Binomial Theorem
• Cube Root Function - Required a fairly un-obvious pattern recognition and the Difference of Cubes special factoring formula.

• We discussed the "Making Quizzes Optional" plan. People mostly wanted Strategy 1. It's less work to just go with that, for me.

We discussed...
• ... some set notation and logic stuff in a quick, informal, and over-everyone's-heads sort of way.
• ... the finer points of intervals of increase/decrease, and why we include the endpoints.
• ... using the linear regression function for 1.2 #6. It turns out the WebAssign will accept the solution line, as long as the coefficients are within 1% of what they should be, BUT if you don't follow their EXACT instructions on how to round those coefficients and you USE that "OK answer" to calculate new outputs using that "slightly off" answer, then your outputs won't be within the tolerance of the algorithm.

  WebAssign accepted -0.000105357x+14.521428 as your linear model, but if you used that exact model, the answer you got by plugging in x = 85000 was wrong. The CORRECT answer for the model was -0.000100x+14.521429.

  View a PDF of the spreadsheet used for the linear regression question.
  Download a working Excel copy of the spreadsheet.

• ... how to use Desmos to enter and evaluate a function.

• We showed how to graph 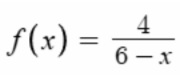, which is just a transformed .

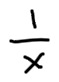  Then we computed some secant slopes fairly efficiently, using Desmos. The idea was to take the x-values closer and closer to x = 7 to see what the instantaneous slope will likely be.

  Finally, we computed the instantaneous slope of f(x) at x = 7.

  Then I wasted time talking about my bad knees. Sorry.

  Fact: If the limit of the difference quotient exists, then plugging in numbers really close to the limiting x-value will get you very close to the instantaneous slope. It's always a good check, but of course, we're going to try to teach you to find its exact value by taking limits.

• Left and right limits. Limit laws. Different styles of limit-taking. Infinite limits.

  Handling absolute values in limits and elsewhere.

  Tangent Problem. Tangent Line. My (preferred) way of writing equations of lines as quickly and efficiently as possible. (Better version of point-slope than the one taught in books and by most teachers.

  Several different ways of expressing the difference quotient. I still want to do an "x - c" version of the limit of (f(x+h)-f(x))/h = (f(c)-f(x))/(c-x).

  We found the equation of the tangent line to the square root of x at x = 16, and we drew the picture for the situation.

  Only scientific calculators permitted (actually REQUIRED) on tests.

  After everybody but one of you left, I was asked a question about 1.3 #11, which in the notes (and hence the videos) is #25.

• I ran over different variations on difference quotients related to the last exercise on the Week 2 Written Assignment.

  I also tried to give people some ideas on how to break trail on new math knowledge. A way to get out of the box you might not realize you put yourself in.

  I keep saying learning is a writing process, and I believe it is, when it comes to learning abstract or complex concepts. I see so many students who try to turn in their first pass at the work, which is slow, laborious, and leads to lower-quality final product.

  You want to be "fast and loose" when you're hitting it the first time. Then, as you figure things out, you can begin writing that "final draft" to be turned in for assessment, and as a touchstone for your own review of the material in the future.

  The better your "final draft," the better of a learning tool it becomes. Also, the better you write it up, the more the knowledge goes into your brain. The act of doing a good writeup reduces the amount of review you need, and it makes that review go much more quickly.

February

• A quick introduction to Section 1.7, followed by some flailing around. *sigh* My eyes are letting me down.

  You should be able to prove the limit of a linear function, with delta = epsilon/slope.

  Higher-degree polynomials require more analysis. They will be bonus on tests. delta = min{1,epsilon/number}, where number will be determined by the behavior of the other factor on [c-1, c+1] for x-->c situations.

• We had a question from 1.7 about the limit of a cubic. It was all very "Wolframalpha.com."

  I used that 1.7 #19 as a springboard to the formal proof of the question of a cubic-polynomial limit, which WebAssign assumes you're all too stupid to even see. I don't think that way. I want to see. I want to show you the basic technique for ALL, FORMAL polynomial limits, and that I have done.

• We re-visited 1.7 #19. Nobody could get part b. Not sure what WebAssign's trying to accomplish with this one, but finding
  f(x) = L + epsilon and f(x) = L - epsilon, for fixed epsilon was fairly straightforward with Desmos.

• Boy we covered a lot! I talked for over 30 minutes straight.

  This was the last lecture before Quiz 1. I posted a video on how that works from the student perspective: Download and Install Lockdown Browser.

  If you're using an Aims laptop, it's already installed.

  I talked almost the entire time. Sorry about that. We covered:

  • Infinite limits
  • Bye-Bye Shots for Quizzes
  • An application of The Squeeze Theorem
  • Manipulating quadratic functions and equations by completing the square
Also included in the notes are screenshots of my Desmos session.

• We extended Quiz 1 deadline to midnight, tonight.

  We did a poor man's intro to Chapter 2, talking about rates of change and derivatives.

  The talk kind of slopped over between 2.1 and 2.2, which are this week's topics. Section 2.2 sort of streamlines 2.1. Then we'll do a LOT of streamlining in 2.3. The sooner we can get to 2.3, the sooner you will really start to see the power of this calculus stuff, because there are a million shortcuts to computing these limits of difference quotients.

• I briefly discussed some random concepts covered on the Week 4 Written Assignment.

  Phoenix asked about the "cheat" for finding derivatives given in notes and videos. I consider the 2.3 and later stuff will be the way we do derivatives in the sequel. You just had to build your chops on limits, first, so you're not just plugging into formulas with no rhyme or reason.

  I went on about the topologist's sine curve (again), trying to show how you might go about proving a limit does NOT exist, by showing you a function where the definition breaks down.

• I remarked on how slow people are to get started on Chapter 2 stuff. I'm really trying to push more active learning. It's more efficient learning. It's deeper learning. We become more like colleagues, where I'm more of a mentor than a high priest for the Math gods.

  I sneaked (snuck?) Section 2.3 concepts in, today. Differentiation Rules "sneak preview." Can save a lot of time finding derivatives, although we're still working on our algebra-and-limits chops at the foundation of everything.

  Did some sum-and-difference-of-cubes stuff. How to apply it to differentiating cubic functions and cube root functions.

  Introduced Liebniz notation (d/dx) and pointed out that it's a "linear operator," taking us from the power rule to a rapid way to evaluate derivatives of any polynomial.

  Finally, I did some sketches of functions and the tangent line to them at a specified point. I got so caught up in the mechanics of the limits that I never did get around to sketching the cube root function and its tangent line at x = 2. I did, however find the equation of the tangent line.

  I spent some time demonstrating and talking about graphing quickly. It's more of a drafting process, where you rough it in, very rapidly, and then re-do the rough sketch, with key points emphasized and nonessential details ignored ("The highest order of human intelligence is knowing what may safely be ignored!").

• We discussed notation issues in the writing of limits, and that "=" is not the same as "-->".

  New, "50% Off" late written work. You have all semester to turn it in, but it will be at a 50% discount, henceforth.

  Work ahead. Even a little bit. Especially a little bit. Have the new section "roughed-in" in your notes ahead of time. You don't have to understand a theorem to jot it down and leave the rest of the page blank, for when we talk about it in class. Even if you don't understand it - especially if you don't understand it - you're creating a place in your brain for the day's talk to go directly into memory, rather than "I'll figure this out at 10 p.m. when it's due at midnight."

  I fought this for years, where student questions were concentrated the day after the homework was due, and I knew for a fact that the class was a lecture behind where it ought to be, and always trying to drag me 2 days behind. I'm looking for students that are pro-active. It's more efficient to be pro-active. 15 minutes that saves you an hour, later....

  sqrt(x)^2 = x. sqrt(x^2) = | x |.

  I worked a Section 2.3 Product Rule exercise, and showed that the WebAssign is satisfied with the form of the answer (unsimplified) that I want to see on tests and homework. If the derivative, itself, is the final product, and we're not doing anything else with it, there's no reason to simplify, other than for practice. When you're under a time control on the Midterm and Final, you don't want to waste ANY time, and that means not simplifying what you don't need to simplify.

  I teased Section 2.4's derivative of the sine function, which is coming to lecture, Monday.

• We discussed a re-scheduling of some of the WebAssign homework, which looks like it's a bit stretched-out just ahead. I want to compress that a little bit, so that we're finishing 2.3 and 2.4 this week and taking a look at 2.5 by Thursday, hopefully.

  We want to leave ourselves some slack for later, in case we need it, and not go too slowly, in the first half of the semester.

  I did some trig review and showed where the proofs of the derivatives of sine and cosine are in the Homework Videos (and Notes) on harryzaims.com (Click here and navigate to Homework Videos (and Notes).

  Some quick trig review was done. I drew a lot of triangles.

• Brief discussion of how 2.3 and 2.4 work together and links to the proofs of the derivatives of the trig functions.

  Re-scheduling some of the WebAssign as we speak. Crazy how it was set up, before.

  Midterm the week after we get back from Spring Break. We get back 3/24 and the Midterm is the following Monday 3/31 or Tuesday, 4.1.

• Not my best Chain Rule speech, but I did lay out how it works. I think the examples at the end, and especially that last one where you have a product rule with 2 chain rule derivatives inside of it, will provide the most practical insight on the matter. It's an (fg)' situation, where both f and g require the Chain Rule to differentiate.

  If I do the formal proof, I'll put it on video in with the 2.5 Homework notes and videos. No one's ever asked.

  The point was made that you shouldn't try to simplify your derivatives unless you HAVE to. Sure, it builds some muscles but the WebAssign isn't that picky and I certainly would prefer to assess the proper application of the differentiation rules than to grade every simplification move, in detail. There are other ways to test for those skills, and I use all of them. "Differentiate. Do not simplify" is not where I'm looking for simplifications. I'll just deduct points for not following instructions and making more work for both of us.

  Right now, I'm poised to lecture WAY ahead of the class, so it's time to dial it back a little bit at my end, and hopefully see the class dial it up a notch and start beating that schedule. I think the more you attack the material that way, the easier it will get to attack new material.

  After I stopped recording, I went radio-silent and drew a bunch of degenerate triangles corresponding to special values of sine and cosine at quadrant angles.

  We'll keep kickin' the can down the road.

Next week, we'll hit 2.5, again. Maybe do the formal proof of the Chain Rule. It's a bit abstract for this level. I'll probably just do a few Chain Rule examples on Monday, and a quick intro to Section 2.6's Implicit Differentiation.

• Boy, I really flubbed the recording, so most of the talk didn't get recorded. I need to come in on time, not early, because I'm too stupid to turn the recording on when I pause it to edit out some of the dead space before class.

  The 2nd video is an example that's almost perfect, except I got a "-" on one term that should be a "+." *sigh* I fixed it in the notes, but I didn't fix the video.

• Today, I pointed out the error I made on the last example. I fixed it in the notes, but not the video from yesterday.

  I also noted that 2 out of 7 of you had actually engaged with Section 2.5 before the 2nd day of the week devoted to 2.5 through 2.7. True mastery comes from hitting the material early and often. A little bit every day. So I worry about folks.

  I worked another 2.5 and another 2.6 exercise, and then cut people loose. Everybody stuck around. Good.

  I mentioned "Lexicon" for word problems (coming up in 2.7). That means a statement defining variables verbally, with the units used for that variable. I'll be working a problem or two from 2.7 on Wednesday.

• We discussed an example involving the modeling of the height (depth) of a tide. I learned some science. I plumb forgot that "2 high tides per day" thing.

  Applications to Natural Science mainly entails applying all we've learned, before in a short lab/science report, wherein you describe the physical situation, define variables and give units, and then, once the model is built, you just do what you've been doing in Calculus.

• We worked #12 from Section 2.7, Implicit Differentiation. It was a y'' question, which we hadn't seen, yet. Took me two tries to get it right the first way I tried.

  Then we looked ahead to next week, and were asked to look at 2.8 and 2.9 before Monday.

March

• We worked some related-rates questions from Section 2.8. Remember, whenever working word problems that you need to create a lexicon or glossary of the variables being used. Describe all variables used in words and give the units.

  I, personally, would not worry about formatting or anything else while I was figuring it out. When I figured it out, THEN I would worry about formatting, lexicon, circling final answers, and such. We're not carpenters. We're writers.

• I worked one more "related rates" exercise, and then proceeded to Section 2.9, Linear Approximations and Differentials. Differentials are just another way of thinking about the tangent line. The f'(a)(x - a) piece of the tangent line L(x) = f'(a)(x - a) + f(a). The (x - a) is the dx = delta x. It measures how far up or down from the original f(a) you are, when you move a distance dx away from x = a.

• We estimated the volume of paint needed for a hemispherical dome of DIAMETER D = 44 meters. I treated the diameter as if it were the RADIUS and my estimates were WAY OFF! For this one, r = 22, not 44!

  Quiz 02 Parts 1 and 2 are coming up. Part 1 is due Sunday, 3/9. Part 2 is due Monday, 3/10. As always, if you don't want to work over the weekend, then get it done before that. I only make due dates on Sunday to give people extra time, if needed.

• We began Chapter 3, with a brief introduction to Section 3.1 - Max and Min Values and Section 3.2 - Mean Value Theorem.. I didn't work any examples from 3.2. I just stated the theorem and pointed out that the theorem doesn't offer a method for finding the c of which the Theorem speaks, but I did state the Main Theorem and drew the picture. A proof of the theorem may be found in the Homework Notes and Videos. I may or may not do a live presentation of the proof. Hopefully, you'll have so many questions, I won't have time for it! LOL!

• We began with the presentation of a word problem from Section 3.2 (Mean Value Theorem). Then somebody asked about Math Shorthand, so there was a listing of a BUNCH of shorthand and a little bit of logic. I remember the logic, but Victor remembered "DeMorgan's Laws," which were discussed, briefly, to tie set theory and logic together.

  I babbled some nonsense about Discrete Math, where I was introduced into basic logic, flow charts, and the like. The highest-level languages are the ones closest to human speech. AI is the ultimate "high-level language," because you write programs just by asking questions! Computer Algebra is a distant second place, but if you understand math language, then you can interact with a CAS on a very high level. The deepest programming is at the machine level. Just remember when people say "low-level language," they're talking about super-geeks who can think in binary and/or hex. High-level computer languages are for people who know little about actual programming.

  Speaking of babbling. Then I went on to prove Rolle's Theorem and Mean Value Theorem, using the Extreme Value Theorem and Fermat's Theorem to do so. Rolle's is used to prove MVT.

• f' > 0 means increasing and f' < 0 means decreasing. 1st Derivative Test.
  f'' > 0 means concave up (smiling) and f'' < 0 means concave down (frowning) 2nd Derivative Test.

  Techniques for building sign patterns and analyzing them for f, f', and f''. I never got past the polynomial and rational-exponent functions, and kind of flubbed the rational-exponent functions due to brain flatulence. The idea was to show an example with a cusp (min/max where f' doesn't exist, but f does) like an x^(2/3) = x^(even/odd) and a vertical spot where the concavity changes, like an x^(3/5) = x^(odd/odd).

  When in doubt, use test values. When you have some intuition/knowledge of a function's behavior, you can build sign patterns on more general considerations, very quickly.

  I didn't quite get to the test-value method. That's good when you're not sure or you just what to check your work.

• ANNOUNCEMENT: Go to Written Work on harryzaims.com. Week 6 and 7 Solutions are posted. If you don't see them, hit refresh (or control-r).

  I really struggled to be coherent, this morning! I spent entirely too much time building a set of examples for class using Maple. I was so tired by the time class started, that I flunked the presentation. I had some good stretches, but also flailed around, pretty much from the start.

  I think that I would have started off better if I had posed that first question on Week 8 Written Assignment better. I have revised both Week 8 and Week 8 Practice to fix that first question. You may want to check out the updated versions. Open them on harryzaims.com and then refresh them.

  I think it's only fair to offer up a set of notes and videos for Week 8 Practice, so that you'll have a much better idea of what you're up against and how to overcome the actual Week 8 Written Assignment.

  Week 8 Practice Videos and Notes - The Notes are now complete. I found my (laws of exponents) mistake on #4 by using the Product Rule for f'', instead of the Quotient Rule via a/b = ab^(-1), so that a/(x-5)^(2/7) = a*(x-5)^(-2/7).

• We had a number of system crashes, today. Everything seems to be working normally, now, but I think maybe I'm just overworking my Smart Notebook that I use to present lectures in class. Maybe it's that sketchy ad-blocker I installed.

  We're almost done with new material that might be on the Midterm. Next time, we'll review for the Midterm, which is scheduled for Monday or Tuesday of next week.

  I learned something new about Desmos. I don't think it will SHOW you the derivative of a function, but it sure does seem happy to GRAPH the derivative. Just write f'(x) and it graphs it!

  We have yet to cover Rational Functions, which is basically what 3.4 is all about. You already have most of the skills. You just need to dredge up memories of College Algebra. The FORMALITIES of 3.4 kind of suck. The PRACTICALITIES of 3.4 are pretty straightforward.

  3.5 is summary of what we're doing, so basically more graphing.
  3.6 is Graphing with calculus and calculators, which we're already doing. So no new theory. Just more examples
  3.7 is optimization problems. Again, nothing new. Just the same stuff, with word problems.
  3.8 is Newton's Method
  3.9 is Antiderivatives.

  I think we can easily cover the ideas and techniques of 3.4 - 3.9 this week, even though some of the assigned work will stretch into next week, after the Midterm (Choose Monday or Tuesday of next week).

• My Internet came back just in time for class. I was a little/lot frenetic, but we managed to discuss rational functions and link you guys up to some examples with videos from College Algebra:
  • Week 9 for College Algebra - #s 3, 4, and 5 are relevant, and there are links provided from each to videos and worked examples.

    We spent some time in class on the #3. Applying Calculus to these guys is pretty hard, without technology. It's good practice, but getting one of these 100% correct, from start to finish, especially when it comes to the 2nd derivative, and finding its zeros!

  ERROR: At the bottom of Page 1 of today's notes, R''(x) is 30/(x-8)^2, not 15/(x-8)^2. (-2)(-15) = 30, not 15 (power rule on -15/(x-8)^2 = -15(x-8)^(-2).

  I found a few errors here and there in the notes and patched most of them up, I think. Then I continued on, computing the 1st and 2nd derivatives entirely by hand, which requires a lot of focus. I didn't mess up until the 2nd derivative, and now I'm giving up on it, as not a good use of my time. LOL!

• I worked a few exercises (limit questions) from last year's midterm. Then I picked up the nasty R(x) we started on Tuesday (3/25). To make the notes flow a little better, the review material at the beginning of the hour was stuck at the end, so they pick up where they left off at the end of Tuesday. The notes from Tuesday were augmented Tuesday afternoon, to try to make it more helpful.

  I messed-up the R'' part of the graph. I knew what I wanted, but I misinterpreted the computer output, and there was an extra inflection point that shouldn't have been there. As I was sketching it, I realized something must be wrong, and that's when I picked up on the extra zero.

  As long as I was copping-out, and resorting to technology, I should have just plugged it into Desmos. I just knew I had it all built in Maple, already, which saved us time watching me typing. I should have remembered there was only one real zero for R''(x). My glaucoma was no help on that one.

  I hope that watching me trouble-shoot my own work is instructive. It is never intentional. I resolve to refrain from making a "I hope everyone learned extra from my mistake" speech. I already wasted enough time making the error!

  By the end of the hour, we had a pretty good idea of what R looked like, including the location of its inflection point, which College Algebra students cannot discern, but we who've taken Calculus I, can. With a lot of work, we can find inflection points, and other features of the graph (like extreme values). We also saw how technically difficult it is to apply all of the techniques to functions that are at all complicated.

  I think it's reasonable to ask you to take derivatives of rational functions of fair complexity, with the injunction "Do not simplify." I just need to see that you fully understand the rules and can write them out, symbolically. If you can do THAT, then I'm pretty confident that you could simplify it by hand, and therefore know exactly how to tell a computer how to do it, and interpret what the computer's saying.

  The Midterm will contain nothing from the "Computers and Graphing Calculators" section in Chapter 3, because neither are permitted on a written test. We're looking to see if you can WRITE it.

  Because you're only allowed a scientific calculator, the most I might do to you is have you sketch the asymptotes of the function, and give a College-Algebra-level rendering of "nice" rational functions.

  I think it's fair to test up through Section 3.5. That's the pacing of the WebAssign work. I know I've been lecturing ahead of where people are, but I really want to put bonus on the Midterm that is drawn from 3.6 - 3.9. Hopefully, I'll re member to work those last two questions on Week 9 Assignment. The sooner I show you both 3.8 and 3.9, the more likely you'll really understand them by the time 3.8 and 3.9 are due, late next week.

  Watching me slog through the R(x) example, stretched over 2 class periods, you've seen pretty much everything that 3.5 is trying to do. What is a complete graph? It's basically the application of everything we know from College Algebra, Trigonometry, and Calculus to give as faithful a rendering of the graph of f(x). Intercepts, asymptotes, local extremes, inflection points, and concavity.

  There'll also be a bonus question on optimization. Use 1st- (and/or 2nd-) deri On the Midterm review, I tried to work them 2 ways. A lot of people on the epsilon-delta know how to find the delta, but don't know what a proof is. Quite. But if you make --> into <--> on your steps, you're pretty close to a proof. I tried to demonstrate it, and it was hard not to write them like I've written them for 35 years. But you can see the bi-directional arrows in one version of the proof.

  Yes, expect a Squeeze Theorem question. Something like showing x*sin(1/x) being continuous at x = 0, or the like. Proving (x^2)*sin(1/x) is differentiable or that x*sin(1/x) is not differentiable would be likely as bonus, long as we're talking about "The Topologist's Sine Curve."

• I worked the last two problems on Week 9. These were based on Section 3.8 and 3.9. Problems based on 3.8 and 3.9 are in the bonus section of the midterm.

  There's a span of a few minutes where I was sharing one screen and working on the other. I went back over the stuff I covered on the wrong screen. Sorry about that.

  We discussed some of Week 7 and Week 8 problems.

  Midterm Open Dates and times:

  Show up any time between 8 am and 6 pm, Monday, 3/31 or Tuesday 4/1. Bring Photo ID, Pen or pencil, one page (2-sided), a scientific calculator, and maybe a ruler or straight edge.

April

April Week 1

• Today, I worked a few optimization problems from Section 3.7. I messed-up the "Make a circle and a square out of 20 m of wire" question. Getting too cute with my arithmetic, and rushing to do it by hand, instead of taking my time and getting it RIGHT.

  I also worked a Newton's Method-type question from Section 3.8 and I uploaded the spreadsheet I used. Once it's programmed, it's child's play to edit 2 cells for f(xn) and f'(xn), and then fill down from those 2 cells. I think this can really speed up your 3.8 work.

• We began with anti-derivatives, starting with The Power Rule, which works for every power of x, except n = -1. We built up a number of trig antiderivatives by working a table of the the trigonometric derivatives we already know, in reverse. We don't have antiderivatives for tan(x), cot(x), csc(x), or sec(x).

  Then the discussion diverged to the case n = - 1, the only power of x to which The Power Rule doesn't apply. It turns out that the power n = - 1 case is the key to rounding out the rest of the trigonometric antiderivatives! Without proof, I claimed that the antiderivative of 1/x is ln|x| + C. Then I reasoned from that as-yet-unproven fact to the anti-derivative of tan(x), to give the class a taste of what was to come, but we won't get to that until Chapter 5 or Chapter 6.

  We finished with a clean-up of Week 9 #9. It seems as though the cosine just "got up and left the room." This results in an unglier-looking answer than my solutions, with a "cos(1)" appearing in the final answer.

April Week 2

• I spoke briefly about Riemann Sums, to kick off Chapter 4, where we introduce the Definite Integral and the 1st and 2nd Fundamental Theorems of Calculus. Anti-Derivatives will figure prominently.

  We discussed where we are, and that the Chapter 3 Quiz is due this week. I gave the day off, so people could take that Quiz 3. I also talked about Quiz 3 Bye-Bye Shot, which is just another version of Quiz 3 that you can take, to try to improve your Quiz scores. Bye-Bye Shots don't always help, but they never hurt, except you're out the time you spent taking them.

  No Week 10 Assignment.

  There will be a 4.1 - 4.4 type assignment. I'm just not quite sure how I'm going to break it up, until I see if people have it in them to plow ahead of schedule or not. I really want the last week or two to be somewhat slack, so you can home in on things you're shaky on. Stuff about Chapter 4, which the schedule says we aren't covering until next week. I just don't see that much new to say about Chapter 3, and I've already asked you 3.8 and 3.9 questions on the Week 9 Assignment.

• Today, I shared links to the Midterm Test and Midterm Solutions.

  I also shared the link to the Chapter 4 Notes and Videos,wherein the theory is presented, and - as always - most exercises are presented as examples.

  I told everybody there that I will happily explain anything they aren't getting, including some of the more tedious Riemann-Sum questions from 4.1 and 4.2. NObody wants to estimate area under a curve by making 10 rectangles. 3 or 4 rectangles is plenty to give you the idea and convince you it were better to learn calculus than to do these estimates.

  Attendance was low. No hardship for me, but when all you have to do is show up, briefly, for the scheduled meeting time, it seems like a silly way to lose points.

• We talked about evaluating polynomials up to degree 3 by the definition of the definite integral, i.e., as the limit of a Riemann Sum.

  I'll work up the Maple, rather than fumbling around in class to "help" people get their work done. This may help you to see the symbolic approach, but I really think I should've done DESMOS.

  Towards the end of the hour, Mark suggested doing a sum on Desmos, and that's what I should have done from the start. Thanks, Mark! It turns out you can tell it to evaluate a sum. It will do all the n = 3, 6, 10, or however many, with some paper and pencil work.

  Drop me a line. Tell me how it's going and/or what you need some help with.

  Python users: Phoenix did those ugly sums with some Python code.

  I applied the 2nd Fundamental Theorem of Calculus to check some of our work. It was all very informal. For the formalities as well as the practical, I think the homework notes and videos cover what we're doing, and class time is more for questions. I just need to know when to shut up!

• We did some Riemann Sums and Definite Integrals with Desmos, using "sum" and "int" commands.

  We discussed FTC I and the Chain Rule version of FTC I. We also used FTC II to check our work.

  We talked about "Net Change" versus "Total Change."

April Week 3

• We kicked it off with a bad explanation of a midpoint-method Riemann Sum. The first thing out of my mouth was correct, but I didn't like the explanation. Today's notes give Victor's question a better treatment.

  We worked a few problems from the Midterm. We want to cover 4.5 this week, but I think that much of 4.1 - 4.4 is already covered.

• I did a lot of grumbling about testing centers. Snipped that part.

  Today was all about Section 4.5 - Integrating by u-Substitution. Adding Chain Rule machinery and concepts to what we know about the definite and indefinite integral.

• I worked a few u-Substitution exercises from the book. All of them were definite integrals.

  I messed up pretty badly, not reading my own writing. A '9' became a '5,' which made the problem a lot messier.

  Then my answer disagreed with Desmos. That's when I picked up on the '9' became '5' thing. '9' was a whole lot better, because the square root of '9' is '3.' The square root of '5' is just the square root of '5.'

  We all agreed at the end that being cruel to dogs is bad, and the owner should be punished if their dog bites someone.

• Finally got all the Midterms graded. It took a long time, because I don't do "double jeopardy." The next work is always based on the assumption that the previous work is correct.

  Many concerning algebra-skills gaps and/or poor techniques that someone taught you before you got to calculus. I hope we can clean some or all of that up, because you need to be STRONG in algebra to succeed going forward in calculus.

  Biggest concern was Quadratic Equation technique. Do the discriminant, first. Simplify its square root. THEN plug into the quadratic formula.

  Test will be averaged over 125 points. Everybody gets 5 points I didn't give them when grading, because the name was worth 5 points.

April Week 4

May

May Week 1

May Week 2