#1 - Polynomial 

#2 - Rational Function with an Oblique Asymptote 

#3 - Another Rational Function (Less Going on.) 

#4 - ANOTHER Rational Function.  More Algebra-type skills. 

#5 - Yes.   Another Rational Function. 

(5.1)

 

(5.2)

 

(5.3)

 

(5.4)

 

(5.5)

 

(5.6)

 

(5.7)

 

(5.8)

 

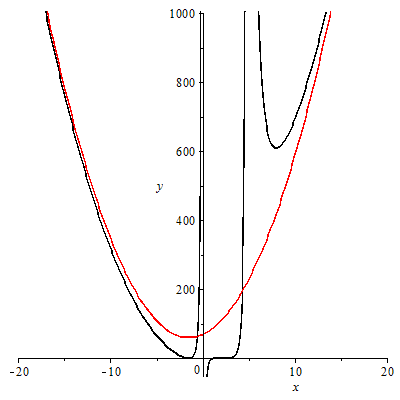
The above is the oblique asymptote.  The following is the remainder upon division. 

(5.9)

 

#6 - A rational function with domain all real numbers. 

(6.1)

 

(6.2)

 

(6.3)

 

(6.4)

 

(6.5)

 

(6.6)

 

(6.7)

 

So no real roots in the denominator. 

#7 - A function with some rational-function features. 

(7.1)

 

(7.2)

 

(7.3)

 

(7.4)

 

(7.5)

 

(7.6)

 

(7.7)

 

(7.8)

 

(7.9)

 

(7.10)

 

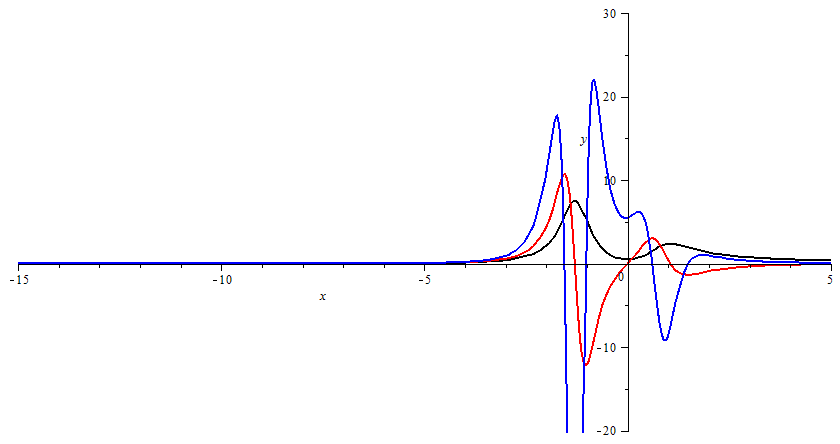
(7.11)

 

#8 - A radical function with a sine inside. 

#9 - Explore a family of cubic polynomials