An MS Word version of
this document...
1. (8
pts)† Form a polynomial of degree 5, with
a zero of multiplicity 1 at x = -3, a
zero of multiplicity 2 at x = 4, and
a zero of multiplicity 1 at x = 1 + 3i .†
Please leave it in factored form.
2. 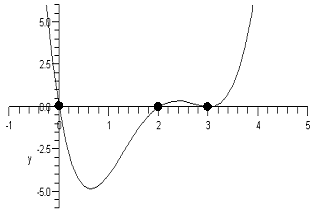 (7
pts)† Circle the polynomial functions in
the list which might have the given graph.
(7
pts)† Circle the polynomial functions in
the list which might have the given graph.
3. (7
pts)† Find the domain of 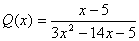 .
.
4. Solve
each of the following inequalities.† The
answers †should †be strangely similar,
yet distinctly different.
a. (5
pts)† 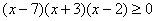
b. (5
pts)† 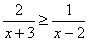 †
†
5. (7
pts)† Use the Remainder Theorem and synthetic division to evaluate 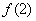 †for
†for  .
.
6. (7
pts)† Use Descartesí Rule of Signs to determine the possible number of
positive and negative real zeros of 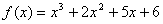 .† You donít need to
find any of the zeros.
.† You donít need to
find any of the zeros.
7. (7
pts)† Use the Rational Zeros Theorem to list all
the possible rational zeros of† 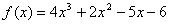 .† You donít need to
find which ones (if any) actually work.†
Just list the possibilities.
.† You donít need to
find which ones (if any) actually work.†
Just list the possibilities.
†
8. (7
pts)† Use the Intermediate Value Theorem to show that 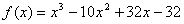 †has a zero in the
interval
†has a zero in the
interval 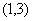 .
.
9. Let
 .
.
a. (5
pts)† Find 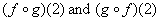
.
b. (5
pts)† Find the domain of the composite
function 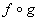 .
.
10. (5
pts)† Given that 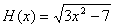 , find functions† f †and †g†
such that
, find functions† f †and †g†
such that 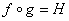 .
.
11. (10
pts)† Find all complex zeros of 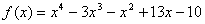 .†
.†
12. (5
pts)† Use the complex zeros from #10 to
write 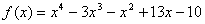 †in factored form.
†in factored form.
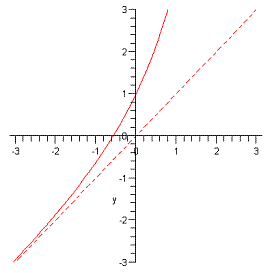
13. (10
pts)† The graph of a one-to-one
function† f† is given.† Draw the graph of the inverse function  .† For convenience (and
as a hint), the graph of
.† For convenience (and
as a hint), the graph of 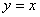 †is given.† (This one is fairly tricky).
†is given.† (This one is fairly tricky).
Bonus Page.
(5
pts)† Find a bound on the real zeros
of 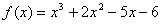 .
.
(5 pts)† Let 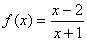 .† Find
.† Find 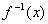 .
.
 (7
pts)† Circle the polynomial functions in
the list which might have the given graph.
(7
pts)† Circle the polynomial functions in
the list which might have the given graph.