1.
(5
pts) 
2.
(5
pts) 
1.
(5
pts)
2.
(5
pts)
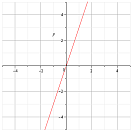
(4 pts) Determine which of the following
functions are one-to-one. Indicate
by writing “Yes” or “No” on the graphs.4.
(10 pts) Solve 
5. (10 pts) Write an exponential function to model the situation. Tell what each variable represents. A population of red ants is initially at 100,000 ants and grows (exponentially) at 20% per week.
6.
(5 pts) Write
the equation 
in exponential form.
7.
(5 pts) Evaluate
.
8.
(10 pts) Express
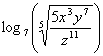in terms of logarithms
of x, y, and z.
9.
(10 pts) Solve
correct to four decimal places: 
10. (5
pts) Solve: 
11. (5
pts) Find the value of the
expression: 
12. (5
pts) Graph: 
13. (5
pts) Write the following as the
logarithm of a single expression. Assume
that variables represent positive numbers.
14. (5
pts) The population (in millions of
people) of Soretoothistan t years after 2000 is given by 
. If there are 12
million people in Soretoothistan in 2005, find k.
15. Cobalt-60
is a radioactive substance that decays according to the model 
, where A = A(t)
is the amount of cobalt-60 present at
time t (in years).
a.
(5 pts) Find the
half-life of cobalt-60. You may leave
your final answer in terms of 
.
b. (5 pts) To the nearest 10th of a year, what is the half-life of cobalt-60, according to this model? (Base your answer on your result from part a.)
16. (10 pts bonus) The half-life of carbon-14 is (approximately) 5730 years.
a.
Find an exponential model 
that gives the amount
of radioactive carbon-14 present in a charcoal sample after t years.
b. How old is a sample from a neolithic fire pit if it is found that 19% of naturally-occurring carbon-14 is present in the sample?
17. (5
pts) Solve the equation: 
.