An MS Word version of this document...
1. Test 2-type Find the complex zeros of 
2. Test 2-type Without solving, determine
the character of the solutions of each equation in the complex number system.
a. (2
pts) 
b. (2
pts) 
c. (2
pts) 
3. Solve
each of the following absolute value equations:
a. (2
pts) 
b. (2
pts) 
4. Solve
each of the following absolute value inequalities. Give your answer in set-builder and interval notation.
a. (3
pts) 
b. (3
pts) 
c. (3
pts) 
d. (3
pts) 
5. Sketch
the graph of each of the following. Use transformations of the graph of 
to graph each
function.
a. (4
pts) 
b. (4
pts) 
6. Let
.
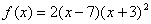a. (2
pts) List each real zero and its
multiplicity.
b. (2
pts) Determine whether the graph crosses
or touches the x-axis at each x-intercept.
c. (2
pts) Determine the behavior of the graph
near each x-intercept.
d. (2
pts) Determine the maximum number of
turning points on the graph.
e. (2
pts) Determine the end behavior; that is, find the power function that the
graph of f resembles for large values
of 
.
f. (5
pts) Use the information from the above
to give a rough sketch of the graph of 
. 2 bonus points for
including the y-intercept.
7. Find
the domain and all asymptotes (vertical, horizontal, oblique) for each of the following rational functions.
a. (5
pts) 
b. (5
pts) 
8. Sketch
the graph of each of the following rational functions, using transformations.
a. (5
pts) 
b. (5
pts) 
9. (15
pts) Sketch the graph of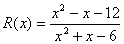 
. Show all intercepts,
asymptotes and holes.
10. Some
followup questions:
a. (5
pts) What is the domain of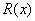 
?
b. (5
pts) What is the behavior of 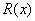near x = 4?
c. (5
pts) What is the behavior of 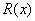near x = 2?