MS Word Version of this document....
Simplify:
1.
2.
3.
Multiply: 
Factor:
4.
5.
6.
Factor:
7.
Solve:
8.
= 25
9.
= 15
10. Solve
by completing the square: 
= 0
11.
Write the expression in the form a + bi:
12. Simplify:
13.
Write the standard form of the equation of the
line passing through the point (1, –5) and perpendicular to the line 
.
14.
Determine the domain and range: 
15. Graph
the parabola and find the vertex: 
16. Determine
the domain of the function 
17. If
f(x) = 
and g(x) = 
,
find 
.
18. 
19. 
³ 18
Graph:
20. 
21. 
22. Solve:
= 
23. Write
the equation 
in logarithmic form.
24. Write
the equation 
in exponential form.
25. Evaluate:
26. Use
the rules for logarithms of products, quotients, and powers to write as the sum
or difference of logarithms: 
27. Solve:
28. f(x)
= 
and g(x) = 
,
find 
.
29. A
radioactive substance decays so that the amount A present at time t
(years) is 
Find the half-life (time for half to decay) of
this substance. 
30. Find
all real solutions of the following equation: 
31. Graph f(x) = 
32. Use
synthetic division to find 
if 
.
33. Use
the Remainder Theorem to find P(–4) if 
34. List
all of the potential rational zeros of the polynomial function. Do not attempt
to find the zeros. 
35. Use the Intermediate Value
Theorem to show that the graph of the function has an x-intercept in the
given interval. Approximate the x-intercept correct to two places.
;
36. Find a third-degree polynomial with real coefficients and with zeros –2 and 4 + i.
37. Find all the real and complex
zeros of the polynomial 
.
Should be able to do this one, but probably too time-consuming for test. But synthetic division to break down a polynomial, given one of its zeros is well within the realm.
38. Find the rational roots of f
. List any irrational roots correct to
two decimal places.
f(x) = 
Rational zeros and Descartes
rule of signs are fair game.
39. Graph
the parabola: 
40. Graph:
41. Find the equation of the circle with center (5, –2) and radius of 2.
42. Find
the vertex of the parabola y = 
.
43. Identify the following curve: 
= 
44. Find the center and radius of the circle with the
following equation: 
45. Graph: 
46. 
47. If
A =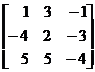 
and B = 
,
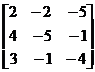find 
.
48. Find the inverse of the matrix
(if it exists) 
.
49. Write
the augmented matrix for the system of equations.
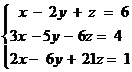
50. Use
matrices to solve the following system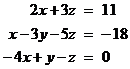 
51. Find the common difference for
the arithmetic sequence: –8, 21, 50, ...
52. Give the first four terms of the
arithmetic sequence for which 
= –38 and d = 3.
53. Write in summation notation:
54. 
– 
+ 
– 
+ 
55. Write as an indicated sum: 
56. Find the common ratio: 
,
,
,
. . .
57. Find
the sum of the geometric series: 
,
,
,
,
. . .
58. Let 
represent the statement:
4 + 12 + 20 + 
+ 
= 
Use the Principle of Mathematical Induction to show that is true for all integers n, 
.
59. Multiply: 
This
type will be bonus.
60. Evaluate: 7!
61. Prestige Builders has a
development of new homes. There are five different floor plans, seven exterior
colors, and an option of either a one-car or a two-car garage. How many choices
are there for one home?
62. Eleven people are entered in a
race. If there are no ties, in how many ways can the first two places come out?
63. How many subsets of two elements
are contained in the set 
64. How many different ways can 9
different runners finish in first, second, and third places in a race?
65. The probability of getting an A
in Mrs. Ritchie's class in any semester is 19%. What is the probability of not
getting an A?
66. Two urns each contain yellow
balls and green balls. Urn I contains three yellow balls and four green balls
and Urn II contains two yellow balls and four green balls. A ball is drawn from
each urn. What is the probability that both balls are yellow?