An MS Word version of this document (for printing/viewing)
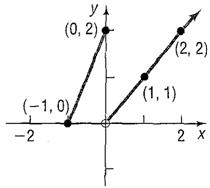
1. (8 pts) Determine whether the relation below represents a function. What is the domain and what is the range?
{(-3,6), (7, 5), (4, 9), (7, 5)}
2. (5
pts) Determine whether the equation ![]() defines y as a function of x. If it does not, show/explain why not.
defines y as a function of x. If it does not, show/explain why not.
3. Let
![]() . Determine the
following, if possible. If not possible,
state why:
. Determine the
following, if possible. If not possible,
state why:
a. (2
pts) ![]()
b. (2
pts) ![]()
c. (2
pts) ![]()
4. (7
pts) Find the domain of ![]() .
.
5. (4
pts) Let ![]() . Find the average
rate of change of f from x = -1 to x = 1.
. Find the average
rate of change of f from x = -1 to x = 1.
6. Let
![]() and
and ![]() .
.
a. (5 pts) Determine the domain of f.
b. (5 pts) Determine the domain of g.
c. Find the following functions and state the domain of each.
i.
(3 pts) ![]()
ii.
(3 pts) ![]()
iii.
(3 pts) ![]()
7. Determine algebraically whether each function is even, odd, or neither.
 The
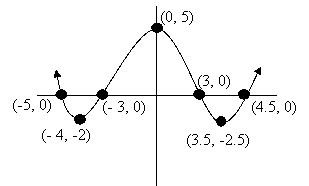
intercepts (Express answers in ordered pairs.
The
intercepts (Express answers in ordered pairs. .
.