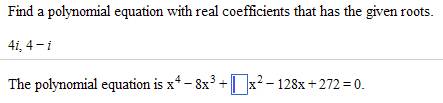
is the factored form of the desired polynomial. Note that each nonreal root is paired with its conjugate. That's what guarantees we'll get rid of all the i 's when we expand the product.

The whole rest of the question is to hone your "bookkeeping" skills. Pure mechanics. They're just looking for the 16 that goes in the box. On a TEST, I'm looking for the factored form, above. There will be a separate question on the mechanics of multiplying complex numbers and terms with nonreal coefficients.

Here's a trick for doing these quickly: Remember that

.

Do the above as a drill, until you instantly recognize that ,

and that it comes from the difference of squares factoring formula (without the ):

,

which I assume, as a college algebra instructor, that all students know like the back of their hands. It's when these patterns are drilled into your skull that you start looking for these things, and even building them, when it suits your purpose.

Anyway, let's see how often we can exploit the formula for :

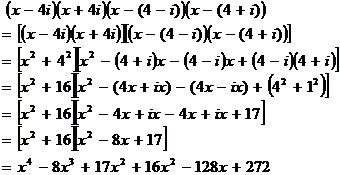
if my arithmetic's correct. It looks like I used the thing twice, in there, once for , and once for .